The Wiener process is not well suited to describe the random path of a financial instruments because the distribution of the step size is time independent. However, the variation of financial assets like the stock price depends on the absolute value of the stock. This means it is more suitable to model the relative variation of the financial asset as a Wiener process.

For the absolute value it leads to the Geometric Wiener process.

b _y denotes the risk less interest rate. The solution of the above stochastic differential equation is the Geometric Wiener process:

y(t) can be seen as a stochastic variable. Realizations of y(t) are representations of the process. The expectation value for y(t) can be computed using the generating function resulting in the risk free interest of the asset.

We now take the natural logarithm of the stochastic process y(t) which results in Wiener process x(t) with drift (b _y-a /2).

Its probability distribution function f_x(t) for x(t)is the one of a Wiener process with drift (b _y-a /2):

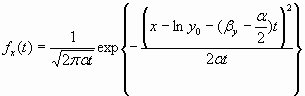
The probability distribution function f_y(t) for the geometric Wiener process itself is the log-normal distribution.